Calibrating Neural Networks

Motivation

Neural networks output "confidence" scores along with predictions in classification. Ideally, these confidence scores should match the true correctness likelihood. For example, if we assign 80% confidence to 100 predictions, then we'd expect that 80% of the predictions are actually correct. If this is the case, we say the network is calibrated. Modern neural networks tend to be very poorly calibrated. We find that this is a result of recent architectural trends, such as increased network capacity and less regularization.

There is a surprisingly simple recipe to fix this problem: Temperature Scaling is a post-processing technique which can almost perfectly restore network calibration. It requires no additional training data, takes a millisecond to perform, and can be implemented in 2 lines of code.

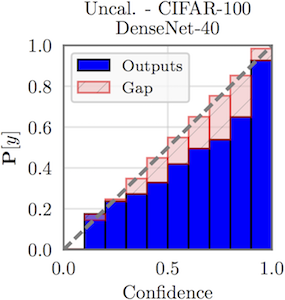
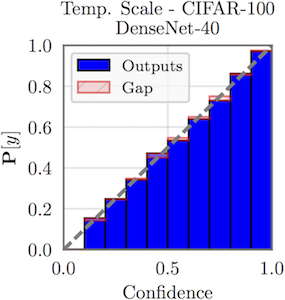
A simple way to visualize calibration is plotting accuracy as a function of confidence (known as a reliability diagram). Since confidence should reflect accuracy, we'd like for the plot to be an identity function. In the reliability diagram above on the left, we see that a DenseNet trained on CIFAR-100 is extremely overconfident. However, after applying temperature scaling, the network becomes very well calibrated.

What is Temperature Scaling?

For classification problems, the neural network output a vector known as the logits. The logits vector is passed through a softmax function to get class probabilities. Temperature scaling simply divides the logits vector by a learned scalar parameter, i.e.

where ... is the prediction, where ... is the logit, and ... is the learned parameter. We learn this parameter on a validation set, where ... is chosen to minimize negative log likelihood. Intuitively, temperature scaling simply softens the neural network outputs. This makes the network slightly less confident, which makes the confidence scores reflect true probabilities.

References

This work is introduced in:

Guo, C., Pleiss, G., Sun, Y. and Weinberger, K.Q. On Calibration of Modern Neural Networks. In ICML, 2017.

• Paper on ArXiV
• BibTeX
• Video of ICML talk

Code

Temperature scaling can be added incredibly easily to any model. In PyTorch for example, add the following to a model after training:

class Model(torch.nn.Module):
    def __init__(self):
        # ...
        self.temperature = torch.nn.Parameter(torch.ones(1))

    def forward(self, x):
        # ...
        # logits = final output of neural network
        return logits / self.temperature
                

Then simply optimize the self.temperature parameter with a few iterations of gradient descent. For a more complete example, check out this PyTorch temperature scaling example on Github.

FAQ

Does temperature scaling work for regression?

Temperature scaling only works for classification. On regression probles, networks tend to output only point predictions, so there is no measure of uncertainty to calibrate.

Can temperature scaling be used to detect adversarial examples?

Temperature scaling works when the test distribution is the same as the training distribution. Since adversarial examples don't belong to the training distribution, temperature scaling is not guarenteed to produce a calibrated probability on these samples.

Why is temperature scaling a post-processing step? Can you find the temperature during training?

The temperature parameter can't be adjusted at training time. The network would simply learn to make the temperature as low as possible, so that it can be very confident on the training examples. (This is why miscalibration occurs in the first place.)